I created this to store passwords in a more secure manner. It could be used to encode a password, and also to retrieve and decode a password. I do permutations based upon a specified number to perform the shift in ASCII (polyalphabetic substitution cipher), but…I’d also like to add a more advanced method, which would increase the complexity of encoding using multiple formulas based upon positioning. As this will be considered v1, I’ll post v2 when complete.
Screenshots
Option Explicit
Dim ASCII_Code1, returnASCII, returnCharacterPermutation, concatenateASCIIPermutation
Dim addPermutation, concatenateASCII, concatenatePermutation, password, iStep, Permutation1
Dim reversePermutation, returnCharacterPermutation2, concatenateASCIIPermutation2, returnLength
Dim concatenateASCII2, ASCII_Registry, Permutation2, concatenatePermutation2, PasswordLength, PermutationConstant
''''''''''''''''''''''''''''''''''''''''''''''''''''''
'PASSWORD TO ENCODE
password = "ABC-XYZ-abc-xyz-0987654321-""-!@#$%^&*(){}|\|/?<>,._-+=`~"
'password = "ABCDEFGHIJKLMNOPQRSTUVWXYZ-abcdefghijklmnopqrstuvwxyz-0987654321-""-!@#$%^&*(){}|\|/?<>,._-+=`~"
'PERMUTATION CAN BE CHANGED 1-55
Permutation1 = 3
''''''''''''''''''''''''''''''''''''''''''''''''''''''
'SESSION
PasswordLength = 0
iStep = 0
concatenateASCII = ""
concatenatePermutation = ""
ASCII_Code1 = ""
ASCII_Registry = ""
PermutationConstant = Permutation1
'ENCODES PASSWORD
FOR iStep = 1 TO LEN(password)
ASCII_Code1 = Asc(MID(password,iStep,1))
'num conversion
ASCII_Code1 = CINT(ASCII_Code1)
concatenateASCII = ASCII_Code1 & " " & concatenateASCII
'ADD PERMUTATION
addPermutation = ASCII_Code1 + Permutation1
returnCharacterPermutation = chr(addPermutation)
concatenateASCIIPermutation = returnCharacterPermutation + concatenateASCIIPermutation
concatenatePermutation = addPermutation & " " & concatenatePermutation
Permutation1 = Permutation1 + 1
NEXT
'DECODES PASSWORD - WILL COME FROM REGISTRY
'concatenateASCIIPermutation = regvalue, eventually
'return length of password
PasswordLength = LEN(concatenateASCIIPermutation)
'the permutation numeric is created subtracting 1 from original number
'and adding the total length of the encoded password
Permutation2 = (PermutationConstant - 1) + PasswordLength
iStep = 0
FOR iStep = 1 TO LEN(concatenateASCIIPermutation)
ASCII_Registry = Asc(MID(concatenateASCIIPermutation,iStep,1))
'num conversion
ASCII_Registry = CINT(ASCII_Registry)
concatenateASCII2 = ASCII_Registry & " " & concatenateASCII2
'REVERSE PERMUTATION
reversePermutation = ASCII_Registry - Permutation2
returnCharacterPermutation2 = chr(reversePermutation)
concatenateASCIIPermutation2 = returnCharacterPermutation2 + concatenateASCIIPermutation2
concatenatePermutation2 = reversePermutation & " " & concatenatePermutation2
Permutation2 = Permutation2 - 1
NEXT
'OUTPUT
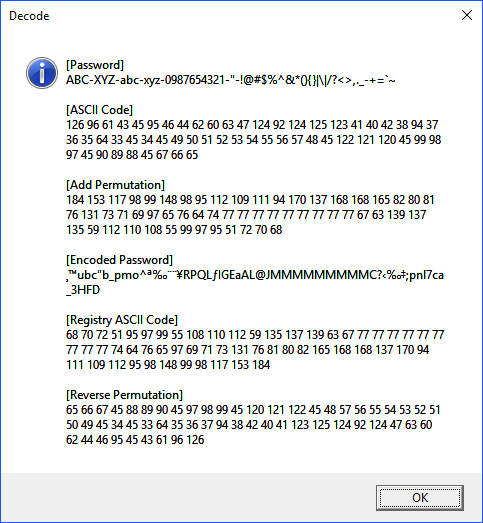
MSGBOX "[Password]" & chr(10) & password & chr(10) & chr(10) & _
"[ASCII Code]" & chr(10) & concatenateASCII & chr(10) & chr(10) & _
"[Add Permutation]" & chr(10) & concatenatePermutation & chr(10) & chr(10) & _
"[Encoded Password]" & chr(10) & concatenateASCIIPermutation & chr(10) & chr(10) & _
"[Registry ASCII Code]" & chr(10) & concatenateASCII2 & chr(10) & chr(10) & _
"[Reverse Permutation]" & chr(10) & concatenatePermutation2,64,"Decode"
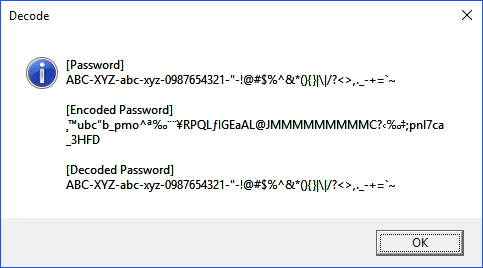
MSGBOX "[Password]" & chr(10) & password & chr(10) & chr(10) & _
"[Encoded Password]" & chr(10) & concatenateASCIIPermutation & chr(10) & chr(10) & _
"[Decoded Password]" & chr(10) & concatenateASCIIPermutation2,64,"Decode"
ASCII_Code1 = ""
returnASCII = ""
returnCharacterPermutation = ""
concatenateASCIIPermutation = ""
addPermutation = ""
concatenateASCII = ""
concatenatePermutation = ""
password = ""
iStep = ""
Permutation1 = ""
reversePermutation = ""
returnCharacterPermutation2 = ""
concatenateASCIIPermutation2 = ""
returnLength = ""
concatenateASCII2 = ""
ASCII_Registry = ""
Permutation2 = ""
concatenatePermutation2 = ""
PasswordLength = ""
PermutationConstant = ""
WScript.Quit(0)
Notes
In v2 (to provide better security for passwords, specifically), what I’m going to do is create unique formulas for each position. It may be written in VB or C#.
So, a potential password, let’s say LetMeIn99$, could look like this once encoded: AAAAAAAAAA.
The idea is that there is zero correlation between one position, to the next, as seen from the onlooker.
From Bruce Schneier’s Applied Cryptography, 2nd edition…
Substitution Ciphers
A substitution cipher is one in which each character in the plaintext is substituted for another character in the ciphertext. The receiver inverts the substitution on the ciphertext to recover the plaintext. In classical cryptography, there are four types of substitution ciphers:
— A simple substitution cipher, or monoalphabetic cipher, is one in which each character of the plaintext is replaced with a corresponding character of ciphertext. The cryptograms in newspapers are simple substitution ciphers.
— A homophonic substitution cipher is like a simple substitution cryptosystem, except a single character of plaintext can map to one of several characters of ciphertext. For example, “A” could correspond to either 5, 13, 25, or 56, “B” could correspond to either 7, 19, 31, or 42, and so on.
— A polygram substitution cipher is one in which blocks of characters are encrypted in groups. For example, “ABA” could correspond to “RTQ,” “ABB” could correspond to “SLL,” and so on.
— A polyalphabetic substitution cipher is made up of multiple simple substitution ciphers. For example, there might be five different simple substitution ciphers used; the particular one used changes with the position of each character of the plaintext.
The famous Caesar Cipher, in which each plaintext character is replaced by the character three to the right modulo 26 (“A” is replaced by “D,” “B” is replaced by “E,”…, “W” is replaced by “Z,” “X” is replaced by “A,” “Y” is
replaced by “B,” and “Z” is replaced by “C”) is a simple substitution cipher. It’s actually even simpler, because the ciphertext alphabet is a rotation of the plaintext alphabet and not an arbitrary permutation.
ROT13 is a simple encryption program commonly found on UNIX systems; it is also a simple substitution cipher. In this cipher, “A” is replaced by “N,” “B” is replaced by “O,” and so on. Every letter is rotated 13 places. Encrypting a file twice with ROT13 restores the original file.
P = ROT13 (ROT13 (P))
ROT13 is not intended for security; it is often used in Usenet posts to hide potentially offensive text, to avoid giving away the solution to a puzzle, and so forth.
Simple substitution ciphers can be easily broken because the cipher does not hide the underlying frequencies of the different letters of the plaintext. All it takes is about 25 English characters before a good cryptanalyst can reconstruct the plaintext [1434]. An algorithm for solving these sorts of ciphers can be found in [578,587,1600,78,1475,1236,880]. A good computer algorithm is [703].
Homophonic substitution ciphers were used as early as 1401 by the Duchy of Mantua [794]. They are much more complicated to break than simple substitution ciphers, but still do not obscure all of the statistical properties of the plaintext language. With a known-plaintext attack, the ciphers are trivial to break. A ciphertext-only attack is harder, but only takes a few seconds on a computer. Details are in [1261].
Polygram substitution ciphers are ciphers in which groups of letters are encrypted together. The Playfair cipher, invented in 1854, was used by the British during World War I [794]. It encrypts pairs of letters together. Its cryptanalysis is discussed in [587,1475,880]. The Hill cipher is another example of a polygram substitution cipher [732]. Sometimes you see Huffman coding used as a cipher; this is an insecure polygram substitution cipher.
Polyalphabetic substitution ciphers were invented by Leon Battista in 1568 [794]. They were used by the Union army during the American Civil War. Despite the fact that they can be broken easily [819,577,587,794] (especially with the help of computers), many commercial computer security products use ciphers of this form [1387,1390,1502]. (Details on how to break this encryption scheme, as used in WordPerfect, can be found in [135,139].) The Vigenère cipher, first published in 1586, and the Beaufort cipher are also examples of polyalphabetic substitution ciphers.
Polyalphabetic substitution ciphers have multiple one-letter keys, each of which is used to encrypt one letter of the plaintext. The first key encrypts the first letter of the plaintext, the second key encrypts the second letter of the plaintext, and so on. After all the keys are used, the keys are recycled. If there were 20 one-letter keys, then every twentieth letter would be encrypted with the same key. This is called the period of the cipher. In classical cryptography, ciphers with longer periods were significantly harder to break than ciphers with short periods. There are computer techniques that can easily break substitution ciphers with very long periods.
A running-key cipher—sometimes called a book cipher—in which one text is used to encrypt another text, is another example of this sort of cipher. Even though this cipher has a period the length of the text, it can also be broken easily [576,794].
Buy book here: Amazon.com — Applied Cryptography